nLab type II supergravity Lie 2-algebra

Idea

A super Lie 2-algebra extension of the super Poincare Lie algebra in $D = 10$ for $N=2$ supersymmetry (as in type II supergravity).

The Chevalley-Eilenberg algebra of the $\mathfrak{sugra}_{typeII}$ (defining it) is that of the $D = 10$ $N = 2$ super Poincaré Lie algebra generated from $\{E, \Psi\}$ with one further generator $B$ in degree 2 and differential given schematically by

$$d B = \big( \overline{\Psi} \Gamma^a \Gamma_{11} \Psi\big) \wedge E_a \,.$$

This is (CAIB 99, equation (6.3)) for type IIA with $N = (1,1)$ and in (Sakaguchi 99 (2.4) and (2.25)) for type IIB with $N = (2,0)$.

It also makes sense to write $\mathfrak{string}_{IIA}$ and $\mathfrak{string}_{IIB}$ for these. See also at string Lie 2-algebra.

Properties

The cocycles of the exceptional ∞-Lie algebra cohomology of $\mathfrak{sugra}_{typeII}$ induce the Green-Schwarz action functional infinity-Wess-Zumino-Witten theory-terms for the D-branes of type II superstring theory (CAIB 99, section 6.1 for IIA and (Sakaguchi 99, section 2) for IIB):

The brane scan.

The Green-Schwarz type super $p$-brane sigma-models (see at table of branes for further links and see at The brane bouquet for the full classification):

$\stackrel{d}{=}$	$p =$	1	2	3	4	5	6	7	8	9
11			M2			M5
10	D0	F1, D1	D2	D3	D4	NS5, D5	D6	D7	D8	D9
9					*
8				*
7			M2${}_{top}$
6		F1${}_{little}$, S1${}_{sd}$		S3
5			*
4		*	*
3		*

(The first columns follow the exceptional spinors table.)

The corresponding exceptional super L-∞ algebra cocycles (schematically, without prefactors):

$\stackrel{d}{=}$	$p =$	1	2	3	4	5	6	7	8	9
11			$\Psi^2 E^2$ on sIso(10,1)			$\Psi^2 E^5 + \Psi^2 E^2 C_3$ on m2brane
10		$\Psi^2 E^1$ on sIso(9,1)	$B_2^2 + B_2 \Psi^2 + \Psi^2 E^2$ on StringIIA	$\cdots$ on StringIIB	$B_2^3 + B_2^2 \Psi^2 + B_2 \Psi^2 E^2 + \Psi^2 E^4$ on StringIIA	$\Psi^2 E^5$ on sIso(9,1)	$B_2^4 + \cdots + \Psi^2 E^6$ on StringIIA	$\cdots$ on StringIIB	$B_2^5 + \cdots + \Psi^2 E^8$ in StringIIA	$\cdots$ on StringIIB
9					$\Psi^2 E^4$ on sIso(8,1)
8				$\Psi^2 E^3$ on sIso(7,1)
7			$\Psi^2 E^2$ on sIso(6,1)
6		$\Psi^2 E^1$ on sIso(5,1)		$\Psi^2 E^3$ on sIso(5,1)
5			$\Psi^2 E^2$ on sIso(4,1)
4		$\Psi^2 E^1$ on sIso(3,1)	$\Psi^2 E^2$ on sIso(3,1)
3		$\Psi^2 E^1$ on sIso(2,1)

The Brane molecule

Furthermore, there exists a more general classification of possible supermembranes in spacetime with $S$ spatial dimensions and $T$ time dimensions, appearing in (Blencowe-Duff 88). In this sense, the brane scan is but the $T=1$ branch of the brane molecule. The objects appearing here are expected to be related to other generalizations of string theory. See D=12 supergravity and bosonic M-theory.

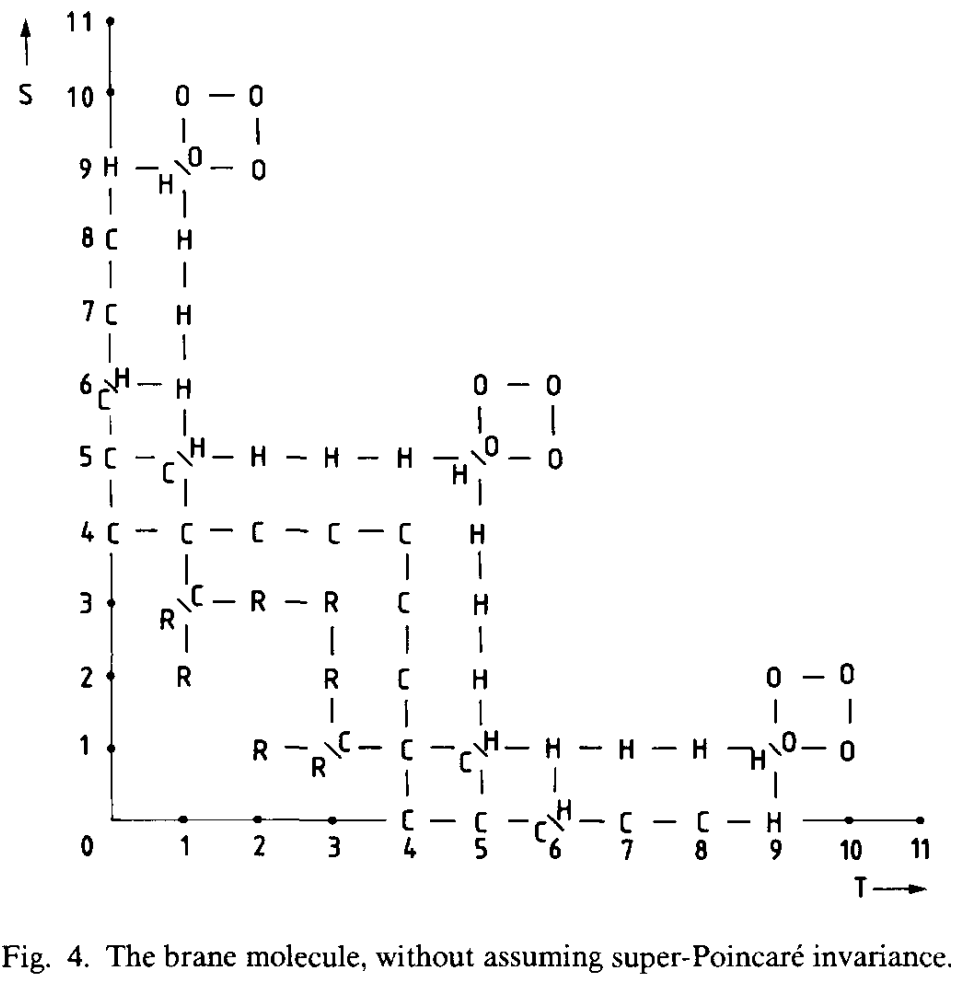
Compare:

• Miles Blencowe, Mike Duff, Supermembranes and the Signature of Space-time, Nucl. Phys. B310 (1988) 387-404 (spire:262142, 10.1016/0550-3213(88)90155-1, pdf)

• brane bouquet

Related concepts

• string Lie 2-algebra

supergravity Lie 6-algebra$\to$ supergravity Lie 3-algebra $\to$ super Poincaré Lie algebra

• type II supersymmetry algebra

References

The type IIA supergravity Lie 2-algebra and its D-brane-Green-Schwarz action functional-type cocycles are discussed in section 6 of

• C. Chrysso‌malakos, José de Azcárraga, José M. Izquierdo, C. Pérez Bueno, The geometry of branes and extended superspaces, Nucl. Phys. B 567 (2000) 293-330 [arXiv:hep-th/9904137, doi:10.1016/S0550-3213(99)00512-X]

The type IIB supergravity Lie 2-algebra and its D-brane-Green-Schwarz action functional-type cocycles are discussed in section 2 of

• Makoto Sakaguchi, IIB-Branes and New Spacetime Superalgebras, JHEP 0004 (2000) 019 (arXiv:hep-th/9909143)

The formulation in super L-infinity algebra theory is in

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields